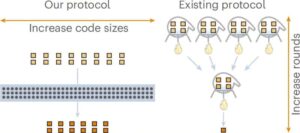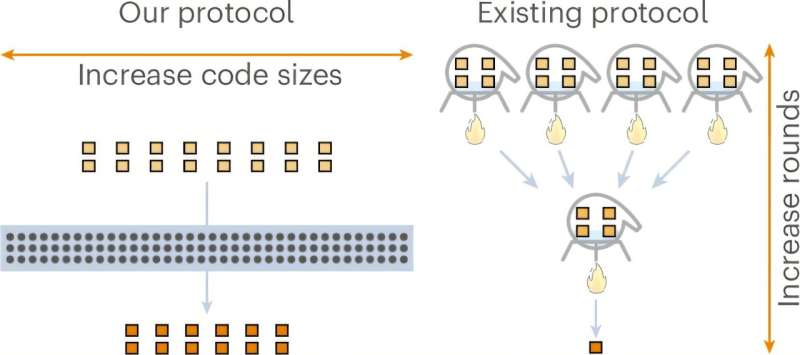
Researchers have made a significant advancement in quantum computing by demonstrating that the theoretically optimal scaling for magic state distillation is achievable for qubits. This breakthrough resolves a long-standing challenge in the field, improving on previous results by reaching a scaling exponent of exactly zero. The findings were published in Nature Physics on November 12, 2025.
Magic state distillation is crucial for achieving fault-tolerant quantum computing. It allows the implementation of non-Clifford operations, which are essential for universal quantum computation. Adam Wills, a Ph.D. student at the Massachusetts Institute of Technology’s Center for Theoretical Physics and the lead author of the study, emphasized the importance of this work. He noted that while building quantum computers is an inspiring goal, the inherent noise and fragility of qubits have posed significant challenges.
Qubits, the fundamental units of quantum information, are highly sensitive to their environment. They require robust error-correcting codes to maintain their integrity during computation. Unfortunately, these codes typically support only Clifford gates, limiting their effectiveness. To overcome this limitation, researchers have turned to magic state distillation, which was first proposed by Bravyi and Kitaev in 2005. This process enables the execution of non-Clifford gates through specially prepared quantum states.
The efficiency of magic state distillation is measured by its overhead, defined as the ratio of input magic states to output magic states required to achieve a specific error rate. A smaller scaling exponent, denoted as γ (gamma), indicates greater efficiency. Historically, reducing this overhead has been a persistent challenge, with the exponent diminishing as error rates improve. Achieving γ = 0 signifies constant overhead, regardless of the quality of the final states.
Wills and his colleagues have demonstrated that achieving constant overhead is indeed possible for qubit systems. Previous research had shown progress, with Hastings and Haah reaching γ ≈ 0.678 in 2017. Subsequent work by Krishna and Tillich approached γ = 0 but required impractically large quantum systems. The new study confirms that constant overhead can be realized, marking a pivotal moment in quantum computing research.
“Constant-overhead magic state distillation is possible,” stated Wills. “If you had a quantum computer that was large enough, accurate enough, and running a long enough algorithm, our methods would be the best way to distill magic.”
The discovery unfolded in two stages, according to Wills. The initial realization was that algebraic geometry codes, a class of error-correcting codes from the 1980s, would be beneficial. Previous attempts had explored other classical codes, but they fell short of achieving the desired efficiency. By applying algebraic geometry codes, the researchers managed to establish constant overhead for 1024-dimensional qudits, which are quantum systems with multiple levels.
The second stage of the discovery involved converting their protocol from qudits to qubits. By interpreting a 1024-dimensional qudit as a set of ten qubits, the team was able to maintain constant overhead with only a slight increase in physical resource requirements. This innovative approach allowed the researchers to demonstrate that constant overhead is achievable for practical qubit systems.
While the theoretical implications of this breakthrough are profound, Wills cautioned that there is still a considerable gap between theory and practical implementation. Achieving γ = 0 scaling is a theoretical ideal, but the physical resources required may exceed what is available in current quantum computing systems.
“The development of a solid theory of quantum magic is crucial for advancing fault-tolerant quantum computing,” Wills noted. “It is common for theoretical work like this to spur multiple practical adaptations in the near term.”
Looking ahead, the research team plans to explore further extensions of their work, including optimizing constant factors and investigating quantum low-density parity-check (LDPC) code variants. They aim to identify the most effective methods for converting qudits to qubits while maintaining efficiency.
This advancement in quantum computing not only establishes a fundamental theoretical limit for magic state distillation but also paves the way for future research aimed at enhancing fault tolerance in quantum systems. The findings underscore the importance of sustained effort in both theoretical and practical realms to realize the full potential of quantum computing.
For more information, refer to the original study by Adam Wills et al., titled “Constant-overhead magic state distillation,” published in Nature Physics.